n NeuroProject / Обучение / Учебник - Зачем нужны аналитические технологии
  Neuroproject.ru / Обучение / Учебник - Зачем нужны аналитические технологии
   Главная / Обучение / Учебник - Зачем нужны аналитические технологии


 
О компании
 Програмные продукты
 Услуги
 Обучение
 Материалы
 Форум
     Учебник       Книги       Java-апплеты       Статьи       Ссылки       Загрузить материалы   
Учебник
Наш учебник

АНАЛИТИЧЕСКИЕ ТЕХНОЛОГИИ
для прогнозирования и анализа данных
Copyright © 1999-2005 НейроПроект

Этот учебник предназначен для первоначального ознакомления с аналитическими технологиями, в частности, с нейронными сетями и генетическими алгоритмами. Он не претендует на научную строгость и полноту. Любые замечания и исправления будут рассмотрены с вниманием.



   Оглавление
   Зачем нужны аналитические технологии
   Нейронные сети
   Генетические алгоритмы
   Методы прогнозирования
   Программные реализации
   Решения практических задач

Зачем нужны аналитические технологии

1. Что такое аналитические технологии

Аналитические технологии - это методики, которые на основе каких-либо моделей, алгоритмов, математических теорем позволяют по известным данным оценить значения неизвестных характеристик и параметров.



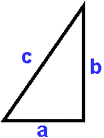Простейший пример аналитической технологии - теорема Пифагора , которая позволяет по длинам сторон прямоугольника определить длину его диагонали. Эта технология основана на известной формуле с2=а2+b2.

Другим примером аналитической технологии являются способы, с помощью которых обрабатывает информацию человеческий мозг. Даже мозг ребенка может решать задачи, неподвластные современным компьютерам, такие как распознавание знакомых лиц в толпе или эффективное управление несколькими десятками мышц при игре в футбол.



Уникальность мозга состоит в том, что он способен обучаться решению новых задач - игре в шахматы, вождению автомобиля и т.д. Тем не менее, мозг плохо приспособлен к обработке больших объемов числовой информации - человек не сможет найти даже квадратный корень из числа 463761 в уме, не используя калькулятора или алгоритма вычисления в столбик. На практике же часто встречаются задачи о числах, гораздо более сложные, чем извлечение корня. Таким образом, человеку для решения этих задач необходимы дополнительные методики и инструменты.



2. Для кого они предназначены

Аналитические технологии нужны в первую очередь людям, принимающим важные решения - руководителям, аналитикам, экспертам, консультантам. Доход компании в большой степени определяется качеством этих решений - точностью прогнозов, оптимальностью выбранных стратегий.



Прогнозирование:

  • курсов валют
  • цен на сырье
  • спроса
  • дохода компании
  • уровня безработицы
  • числа страховых случаев


Оптимизация:

  • расписаний
  • маршрутов
  • плана закупок
  • плана инвестиций
  • стратегии развития

Как правило, для реальных задач бизнеса и производства не существует четких алгоритмов решения. Раньше руководители и эксперты решали такие задачи только на основе личного опыта. С помощью аналитических технологий строятся системы, позволяющие существенно повысить эффективность решений.



3. Традиционные технологии (Детерминированные технологии)

Аналитические технологии типа теоремы Пифагора используются человеком уже много веков. За это время было создано огромное количество формул, теорем и алгоритмов для решения классических задач - определения объемов, решения систем линейных уравнений, поиска корней многочленов. Разработаны сложные и эффективные методы для решения задач оптимального управления, решения дифференциальных уравнений и т.д. Все эти методы действуют по одной и той же схеме.

Для того, чтобы алгоритм был применим, необходимо, чтобы данная задача полностью описывалась определенной детерминированной моделью (некоторым набором известных функций и параметров). В таком случае алгоритм дает точный ответ. Например, для применимости теоремы Пифагора следует проверить, что треугольник - прямоугольный.



Вероятностные технологии

На практике часто встречаются задачи, связанные с наблюдением случайных величин - например, задача прогнозирования курса акций. Для подобных задач не удается построить детерминированные модели, поэтому применяется принципиально иной, вероятностный подход. Параметры вероятностных моделей - это распределения случайных величин, их средние значения, дисперсии и т.д. Как правило, эти параметры изначально неизвестны, а для их оценки используются статистические методы, применяемые к выборкам наблюдаемых значений (историческим данным).



Такого рода методы также предполагают, что известна некоторая вероятностная модель задачи. Например, в задаче прогнозирования курса можно предположить, что завтрашний курс акций зависит только от курса за последние 2 дня (авторегрессионная модель). Если это верно, то наблюдения курса в течение нескольких месяцев позволяют достаточно точно оценить коэффициенты этой зависимости и прогнозировать курс в будущем.





4. Примеры реальных задач

Оптимальное распределение инвестиций

Задача: Имеется инвестиционный капитал, который нужно распределить среди 10 проектов. Для каждого проекта задана функция зависимости прибыли от объема вложения. Требуется найти наиболее прибыльный вариант распределения капитала, при условии, что заданы минимальный и максимальный объем инвестиций для каждого проекта.
Традиционное решение: Чаще всего решение в данном случае принимает руководитель, основываясь только на личных впечатлениях о проектах. Размеры упущенной выгоды при этом не подсчитывают, и неоптимальность решения может остаться незамеченной.
В случае, если руководитель поручает аналитикам выбрать наиболее прибыльный вариант, применяются математические методы оптимизации. Если все данные функции линейны, то можно применить методы линейного программирования (симплекс-метод). Если хотя бы одна из функций нелинейна, то можно использовать метод градиентного спуска или полного перебора.

Прогнозирование курсов акций

Задача: Трейдеру фондового рынка требуется ежедневный прогноз поведения курса акций энергетического предприятия РАО ЕЭС.
Дано: Значения котировок и различных рыночных индикаторов за последний год. Также известны котировки нефтяных и угольных компаний, а также городских компаний-энергопотребителей, которые тесно связаны с курсом акций ЕЭС.
Традиционное решение: Используются методики технического анализа, корреляционного анализа, статистика.



5. Недостатки традиционных технологий

К сожалению, классические методики оказываются малоэффективными во многих практических задачах. Это связано с тем, что невозможно достаточно полно описать реальность с помощью небольшого числа параметров модели, либо расчет модели требует слишком много времени и вычислительных ресурсов.
В частности, рассмотрим проблемы, возникающие при решении задачи оптимального распределения инвестиций.

  1. В реальной задаче ни одна из функций не известна точно - известны лишь приблизительные или ожидаемые значения прибыли. Для того, чтобы избавиться от неопределенности, мы вынуждены зафиксировать функции, теряя при этом в точности описания задачи.
  2. Детерминированный алгоритм для поиска оптимального решения (симплекс-метод) применим только в том случае, если все данные функции линейны. В реальных задачах бизнеса это условие не выполняется. Хотя данные функции можно аппроксимировать линейными, решение в этом случае будет далеким от оптимального.
  3. Если одна из функций нелинейна, то симплекс-метод неприменим, и остается два традиционных пути решения этой задачи.
Первый путь - использовать метод градиентного спуска для поиска максимума прибыли. В данном случае область определения функции прибыли имеет сложную форму, а сама функция - несколько локальных максимумов, поэтому градиентный метод может привести к неоптимальному решению.
Второй путь - провести полный перебор вариантов инвестирования. Если каждая из 10 функций задана в 100 точках, то придется проверить около 1020 вариантов, что потребует не менее нескольких месяцев работы современного компьютера.

Вероятностные технологии также обладают существенными недостатками при решении практических задач. Мы проиллюстрировали работу вероятностного подхода на примере простой линейной авторегрессионной модели, однако зависимости, встречающиеся на практике, часто нелинейны. Даже если и существует простая зависимость, то ее вид заранее неизвестен. Отметим также, что статистические методы хорошо развиты только для одномерных случайных величин. Если же мы хотим учитывать для прогнозирования курса акций несколько взаимосвязанных факторов (например, объем сделок, курс доллара и т.д.), то придется обратиться к построению многомерной статистической модели. Однако, такие модели либо предполагают гауссовское распределение наблюдений (что не выполняется на практике), либо не обоснованы теоретически. В многомерной статистике за неимением лучшего нередко применяют малообоснованные эвристические методы, которые по своей сути очень близки к технологии нейронных сетей. Об этом будет более подробно сказано в следующем разделе.



6. Новые технологии

Из-за описанных выше недостатков традиционных методик в последние 10 лет идет активное развитие аналитических систем нового типа. В их основе - технологии искусственного интеллекта, имитирующие природные процессы, такие как деятельность нейронов мозга или процесс естественного отбора.

Наиболее популярными и проверенными из этих технологий являются нейронные сети и генетические алгоритмы. Первые коммерческие реализации на их основе появились в 80-х годах и получили широкое распространение в развитых странах.

Нейронные сети в каком-то смысле являются имитациями мозга, поэтому с их помощью успешно решаются разнообразные "нечеткие" задачи - распознавание образов, речи, рукописного текста, выявление закономерностей, классификация, прогнозирование.




В таких задачах, где традиционные технологии бессильны, нейронные сети часто выступают как единственная эффективная методика решения. По данным фирмы Ward Systems Group, в 1998 году программные продукты на основе нейронных сетей использовались более чем в 500 крупнейших компаниях мира из списка Fortune 1000.

Генетические алгоритмы - это специальная технология для поиска оптимальных решений, которая успешно применяется в различных областях науки и бизнеса. В этих алгоритмах используется идея естественного отбора среди живых организмов в природе, поэтому они называются генетическими. Генетические алгоритмы часто применяются совместно с нейронными сетями, позволяя создавать предельно гибкие, быстрые и эффективные инструменты анализа данных.




   Оглавление
   Зачем нужны аналитические технологии
   Нейронные сети
   Генетические алгоритмы
   Методы прогнозирования
   Программные реализации
   Решения практических задач


   Учебник       Книги       Java-апплеты       Статьи       Ссылки       Загрузить материалы   


Rambler's Top100 Rambler's Top100